CRISTIAN A FONTALVO: ALGORITMOS

Introducción

La computadora no solamente es una máquina que puede realizar procesos para darnos resultados, sin que tengamos la noción exacta de las operaciones que realiza para llegar a esos resultados. Con la computadora también podemos diseñar soluciones a la medida, de problemas específicos que se nos presenten. Más aún, si estos involucran operaciones matemáticas complejas y/o repetitivas, o requieren del manejo de un volumen muy grande de datos. A las soluciones creadas por computadora se les conoce como programas y no son mas que una serie de operaciones que realiza la computadora para llegar a un resultado, con un grupo de datos específicos. Podríamos decir que un programa es el conjunto de instrucciones escritas de algún lenguaje de programación y que ejecutadas secuencialmente resuelven un problema especifico. Para poder realizar programas, además de conocer la metodología para solucionar problemas, también debemos conocer, de manera especifica las funciones que puede realizar la computadora y las formas en que se pueden manejar los elementos que hay en la misma. El procesamiento de información en la computadora puede representarse así:

1. Metodología para la solución de problemas por medio de computadora:

- Definición del Problema: Esta fase está dada por el enunciado del problema, el cual requiere una definición clara y precisa. Es importante que se conozca lo que se desea que realice la computadora; mientras ésto no se conozca del todo, no tiene mucho caso continuar con la siguiente etapa.

- Análisis del Problema: Una vez que se ha comprendido lo que se desea de la PC, es necesario definir:

· Los datos de entrada.

· La información que se desea producir (salida)

· Los métodos y fórmulas que se necesitan para procesar los datos.

Una recomendación muy practica es el que nos pongamos en el lugar de la computadora y analicemos que es lo que necesitamos que nos ordenen y en qué secuencia, para producir los resultados esperados.

- Diseño del Algoritmo: Consiste en diseñar la serie de pasos organizados que describe el proceso que se debe seguir, para dar solución al problema especifico. Las características de un buen algoritmo son:

· Debe tener un punto particular de inicio.

· Debe ser definido, no debe permitir dobles interpretaciones.

· Debe ser general, soportar las variantes que se puedan presentar en la definición del problema.

· Debe ser finito en tamaño y tiempo de ejecución.

- Codificación: Es la operación de escribir la solución del problema (de acuerdo a la lógica del diagrama de flujo o pseudocódigo), en una serie de instrucciones detalladas (código fuente), en un lenguaje reconocible por la computadora (lenguaje de programación de alto nivel).

- Prueba y Depuración: Los errores humanos dentro de la programación de computadoras son muchos y aumentan considerablemente con la complejidad del problema. El proceso de identificar y eliminar errores, para dar paso a una solución sin errores se le llama depuración.

- Documentación: Es la guía o comunicación escrita en sus variadas formas, ya sea en enunciados, procedimientos, dibujos o diagramas. A menudo un programa escrito por una persona, es usado por otra. Por ello la documentación sirve para ayudar a comprender o usar un programa o para facilitar futuras modificaciones (mantenimiento).

- Mantenimiento: Se lleva a cabo después de terminado el programa, cuando se detecta que es necesario hacer algún cambio, ajuste o complementación al programa para que siga trabajando de manera correcta. Para poder realizarlo se requiere que el programa este correctamente documentado.

2. Lenguajes de programación:

2.1. Lenguaje: Es una serie de símbolos que sirven para transmitir uno o más mensajes (ideas) entre dos entidades diferentes. A la transmisión de mensajes se le conoce comúnmente como comunicación. La comunicación es un proceso complejo que requiere una serie de reglas simples, pero indispensables para poderse llevar a cabo. Las dos principales reglas son:

· Los mensajes deben correr en un sentido a la vez.

· Deben existir 4 elementos: emisor, receptor, medio de comunicación y mensaje.

2.2. Lenguaje de Programación: Es un conjunto de símbolos, caracteres y reglas que le permiten a las personas comunicarse con la computadora. Los lenguajes de programación tienen un conjunto de instrucciones que nos permiten realizar operaciones de entrada/salida, cálculo, manipulación de textos, lógica/comparación y almacenamiento/recuperación. Los lenguajes de programación se clasifican en:

- Lenguaje de Máquina: Sus instrucciones son directamente entendibles por la computadora y no necesitan traducción para que la CPU pueda comprenderlas y ejecutarlas. Las instrucciones se expresan en términos de la unidad de memoria más pequeña: el bit (dígito binario 0 o 1).

- Lenguaje de Bajo Nivel: Ensamblador. Las instrucciones se escriben en códigos alfabéticos conocidos como mnemotécnicos para las operaciones y direcciones simbólicas.

- Lenguaje de Alto Nivel: Visual Basic, C++, Cobol, etc. Las instrucciones son escritas con palabras similares a los lenguajes humanos (en general en inglés), lo que facilita la escritura y comprensión del programa.

3. Traductores de lenguaje:

Los traductores de lenguajes son programas que traducen a su vez los programas fuente escritos en lenguajes de alto nivel a código máquina. Los traductores se dividen en Compiladores e Intérpretes.

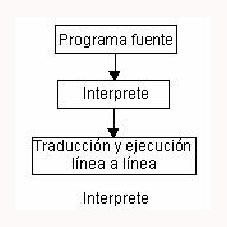3.1. Intérpretes: Un intérprete es un traductor que toma un programa fuente escrito en un lenguaje de alto nivel, lo traduce y lo ejecuta a medida que lo traduce. Es decir, el interpretador toma cada línea del programa, la traduce, la ejecuta y continúa con la siguiente hasta terminar. Un lenguaje que soporta un traductor de tipo intérprete se denomina lenguaje interpretado. BASIC es el modelo por excelencia interpretado; los programas fuente en BASIC se escriben con ayuda de un programa denominado editor que suele venir incorporado al intérprete.

3.2. Compiladores: Un compilador es un programa que traduce un programa fuente escrito en lenguaje de alto nivel a lenguaje de máquina. El programa escrito en lenguaje de alto nivel se llama programa fuente y el programa traducido se llama programa objeto o código objeto. El compilador traduce todo el programa fuente sin ejecutarlo; luego de la traducción la ejecución puede realizarse. Lenguajes compilados típicos son: PASCAL, COBOL y C.

Fases de la compilación: El programa objeto obtenido de la compilación no ha sido traducido a código máquina sino a ensamblador. Para conseguir el programa de máquina real se debe utilizar un programa llamado montador o enlazador (linker). El proceso de montaje conduce a un programa en lenguaje máquina directamente ejecutable. Por ejemplo, la compilación y ejecución de un Programa en C++ tiene los siguientes pasos:

1. Escritura del programa fuente con un editor (programa que permite a una computadora actuar como una máquina de escribir electrónica) y guardarlo en un dispositivo de almacenamiento (un disco).

2. Introducir el programa fuente en memoria.

3. Compilar el programa con el compilador C++.

4. Verificar y corregir errores de compilación (listado de errores).

5. Obtención del programa objeto.

6. El montador obtiene el programa ejecutable.

7. Se ejecuta el programa y si no existen errores, se tendrán las salidas.

4. Programas y algoritmos:

4.1. Programa: Un programa de computadora es un conjunto de instrucciones (órdenes dadas a la máquina) que producirán la ejecución de una determinada tarea. En esencia, un programa es un medio para conseguir un fin. El fin será definido como la información necesaria para solucionar un problema.

4.2. Algoritmo: La palabra algoritmo se deriva de la traducción al latín de la palabra árabe alkhowarizmi, nombre de un matemático y astrónomo árabe que escribió un tratado sobre manipulación de números y ecuaciones en el siglo IX. Un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema especifico. Los algoritmos pueden ser de dos tipos:

- Cualitativos: Se describen los pasos utilizando palabras.

- Cuantitativos: Se utilizan cálculos numéricos para definir los pasos del proceso.

4.3. Lenguajes Algorítmicos: están conformados por una serie de símbolos y reglas usadas para describir los procesos.

Los lenguajes algorítmicos pueden ser:

- No gráficos: Pseudocódigo. Representan en forma descriptiva los pasos que debe realizar un algoritmo para solucionar el problema. El pseudocódigo es una mezcla de lenguaje de programación y español (o cualquier otro idioma) que se emplea, en programación estructurada, para realizar el pre-diseño de un programa. El pseudocódigo usa palabras que indican cada paso del proceso a realizar.

Gráficos: Diagrama de flujo. Representan gráficamente los pasos que debe realizar un algoritmo para solucionar el problema. Esta representación gráfica se dá cuando varios símbolos (que indican diferentes procesos en la computadora), se relacionan entre sí mediante líneas que indican el órden en que se deben ejecutar los procesos. Los símbolos que se pueden utilizar han sido normalizados por el ANSI - Instituto Norteamericano de Normalización.

Ventajas de utilizar pseudocódigo en lugar de diagrama de flujo:

· Ocupa menos espacio en una hoja de papel

· Permite representar en forma fácil operaciones repetitivas complejas

· Es muy fácil pasar pseudocódigo a un programa en algún lenguaje de programación.

· Se pueden observar claramente los niveles que tiene cada operación.

5. Expresiones:

Las expresiones son combinaciones de operandos (datos), operadores (signos de operaciones) y símbolos de agrupación (paréntesis). Ejemplo: a + (b + 3) / c. Cada expresión toma un valor que se determina tomando los valores de los datos implicados y ejecutando sobre ellos las operaciones indicadas, de acuerdo con los símbolos de agrupación y la prioridad que las operaciones tengan entre sí. Según el tipo de operadores que contienen, las expresiones se clasifican en: aritméticas, lógicas y relacionales.

5.1. Operandos: Los datos pueden ser clasificados según la clase de valor que tengan o según la estabilidad de su valor en el tiempo:

- Según la clase de valor: Todos los datos tienen un tipo asociado con ellos, de acuerdo con su valor. Un dato puede ser un simple carácter, tal como ‘b’ o un valor entero tal como 35. Su clasificación es:

Numéricos (enteros y reales)

Simples Lógicos

Alfanuméricos (carácter y cadenas)

Tipos de Arreglos (vectores y matrices)

datos Estructurados Apuntadores

Registros

Archivos

Def. por el usuario (enumerados)

· Datos Numéricos: Permiten representar valores escalares de forma numérica, esto incluye a los números enteros y los reales. Este tipo de datos permiten realizar operaciones aritméticas comunes.

· Datos Lógicos: Son aquellos que solo pueden tener dos valores (cierto o falso) ya que representan el resultado de una comparación entre otros datos (numéricos o alfanuméricos).

· Datos Alfanuméricos: Es una secuencia de caracteres alfanuméricos que permiten representar valores identificables de forma descriptiva, esto incluye nombres de personas, direcciones, etc. Es posible representar números como alfanuméricos, pero estos pierden su propiedad matemática, es decir no es posible hacer operaciones con ellos. Este tipo de datos se representa encerrados entre comillas. Ejemplo: “1997”

- Según la estabilidad de su valor en el tiempo: Un dato puede conservar su valor o pueden ir adquiriendo valores diferentes a lo largo del tiempo. Según ésta, los datos pueden ser:

Constantes Numéricas

Por su Contenido Lógicas

Tipos de Alfanuméricas

datos Variables De Trabajo

Por su Uso Contadores

Acumuladores

· Constante: dato que no cambia su valor durante la ejecución del programa. Ejemplo: a = 3.14

· Variable: espacio en la memoria del computador que permite almacenar un dato; su contenido puede cambiar durante la ejecución del programa. Para identificar una variable en memoria, es necesario darle un nombre con el cual podamos mencionarla en un algoritmo.

Ejemplo: área = pi * radio ^ 2 (variables: radio y área, constante: pi)

· Variable Numérica: almacena valores numéricos, positivos o negativos. Ejemplo: a=0.15

· Variable Lógica: solo puede tener dos valores (cierto o falso). Ejemplo: sw=”F”, res=”V”

· Variable Alfanumérica: contiene carácteres alfanuméricos (letras, números y carácteres especiales). Ejemplo: letra=’a’, apellido=’Lopez’, direccion=’Av. Libertad #190’

· Variable de Trabajo: recibe el resultado de una operación matemática. Ejemplo: suma=a+b

· Variable Contador: controla el número de ocasiones en que se realiza una operación o se cumple una condición; se incrementa generalmente de uno en uno. Ejemplo: cuenta=cuenta+1

· Variable Acumulador: sirve para llevar la suma acumulativa de una serie de valores que se van leyendo o calculando progresivamente. Ejemplo: suma=suma+c

5.2. Operadores: son elementos que relacionan de forma diferente los valores de uno o más operandos (variables y/o constantes). Es decir, los operadores nos permiten manipular valores. Los operadores deben resolverse o evaluarse siguiendo un órden, precedencia o prioridad. Los tipos de operadores que existen son: aritméticos, lógicos y relacionales.

5.2.1. Operadores Aritméticos: +, - , *, /, ^ (exponenciación), mod (módulo, residuo de división entera) y div (cociente de división entera). Los operadores aritméticos permiten la realización de operaciones matemáticas sobre los operandos. Pueden ser utilizados con tipos de datos enteros o reales. Si ambos son enteros, el resultado es entero; si alguno de ellos es real, el resultado es real. La prioridad de los operadores aritméticos es:

	( )
	Λ
	*, /, mod, div
	+, -

Los paréntesis anidados se evalúan de dentro a fuera, el más interno se evalúa primero. Los operadores con igual nivel de prioridad se evalúan de izquierda a derecha en el órden en que aparecen en la expresión.

Ejemplos:

4 + 2 * 5 = 14

23 * 2 / 5 = 9.2

3 + 5 * (10 - (2 + 4)) = 23

3 + 5 * (10 - 6) = 3 + 5 * 4 = 3 + 20 = 23

(1.5 + 3.0 * 4.1) = 28.98

5.2.2. Operadores Lógicos: Λ (y, and, conjunción), V (o, or, disjunción), ~ (¬, no, not, negación). Establecen relaciones entre valores lógicos, que pueden ser resultado de una expresión relacional. La prioridad de los operadores lógicos es:

	~ (¬, no, not, negación)
	Λ (y, and, conjunción)
	V (o, or, disjunción)

Las expresiones con operadores lógicos (proposiciones) se evalúan usando tablas de verdad, que muestran los valores de verdad que puede tener una proposición y las condiciones que los determinan. Una proposición tiene valor verdadero (V) o falso (F), pero no ambos a la vez.

pÙq

pÚq

Øp

Ejemplos para a = “V”, b = “V” y c = “F”:

a V c Verdadero

a Λ ~ b Falso

5.2.3. Operadores Relacionales: >, <, >=, <=, =, < > (diferente). Los operadores relacionales se utilizan para establecer una relación entre dos valores del mismo tipo, comparándolos entre sí para producir un resultado de certeza o falsedad. Los operadores relacionales tienen el mismo nivel de prioridad en su evaluación y tienen menor prioridad que los aritméticos.

Ejemplos para a = 10, b = 20 y c = 30:

a + b > c Falso

a - b < c Verdadero

a - b = c Falso

a * b < > c Verdadero

5.2.4. Evaluación de operadores de tipos diferentes: La prioridad a usar es la siguiente: